Binary to Gray Code Converter

Gray Code is similar to binary code except its successive number differs by only a single bit. Hence, it has importance in communication systems as it minimizes error occurrence. They are also useful in rotary, optical encoders, data acquisition systems, etc.

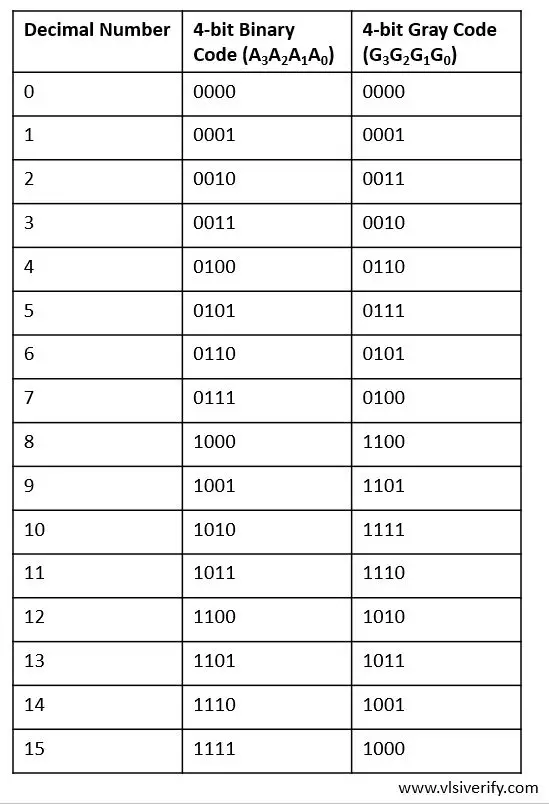
Let’s see binary numbers and their equivalent gray code in the below table.

Truth Table

By solving using K-map technique, a simple combinational circuit turned out as

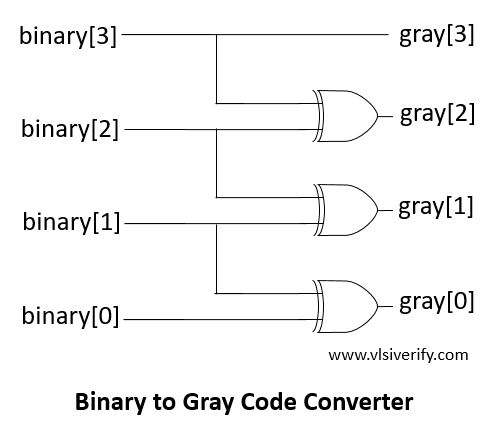
Binary to Gray Code Converter Verilog Code

module b2g_converter #(parameter WIDTH=4) (input [WIDTH-1:0] binary, output [WIDTH-1:0] gray);
  genvar i;    
  generate
    for(i=0;i<WIDTH-1;i++) begin
      assign gray[i] = binary[i] ^ binary[i+1];
    end
  endgenerate
  
  assign gray[WIDTH-1] = binary[WIDTH-1];
endmodule

Testbench Code

module TB;
  reg [3:0] binary, gray;
  b2g_converter b2g(binary, gray);
  
  initial begin
    $monitor("Binary = %b --> Gray = %b", binary, gray);
    binary = 4'b1011; #1;
    binary = 4'b0111; #1;
    binary = 4'b0101; #1;
    binary = 4'b1100; #1;
    binary = 4'b1111;
  end
endmodule

Output:

Binary = 1011 --> Gray = 1110
Binary = 0111 --> Gray = 0100
Binary = 0101 --> Gray = 0111
Binary = 1100 --> Gray = 1010
Binary = 1111 --> Gray = 1000

Compact implementation is mentioned below:

Alternative Verilog implementation

module b2g_converter #(parameter WIDTH=4) (input [WIDTH-1:0] binary, output [WIDTH-1:0] gray);
  assign gray = binary ^ (binary >> 1);
endmodule

Verilog Codes