Tutorials
Learn More
Booth’s Multiplier
In Booth’s multiplier works on Booth’s Algorithm that does the multiplication of 2’s complement notation of two signed binary numbers.
Advantages:
- Less complexity
- Faster Multiplication
- Consecutive additions are replaced
- Ease in scaling
Disadvantage:
- High power consumption
- Large chip area
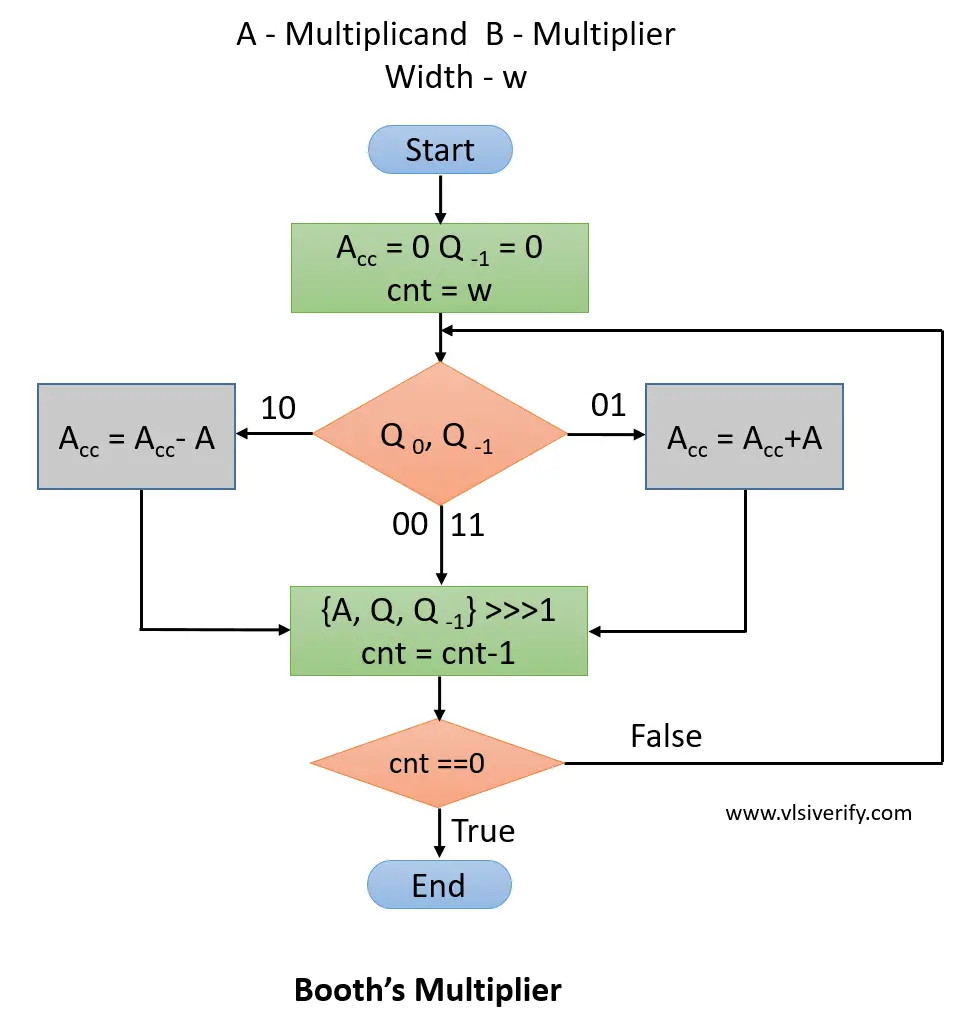
Flow chart of Booth’s Algorithm
Please note of below abbreviations used:
A – holds Multiplicand
B – holds Multiplier
Q = B
Q0 – holds 0th bit (LSB) of Q register
Q-1 – 1-bit variable/register.
Acc – Accumulator holds the result of intermediate addition/subtraction.
Count = max(width of multiplicand register, width of multiplier register)
Booth’s Multiplier Verilog Code
module half_adder(input a, b, output s0, c0);
assign s0 = a ^ b;
assign c0 = a & b;
endmodule
module full_adder(input a, b, cin, output s0, c0);
assign s0 = a ^ b ^ cin;
assign c0 = (a & b) | (b & cin) | (a & cin);
endmodule
module array_multiplier(input [3:0] A, B, output [7:0] z);
reg signed p[4][4];
wire [10:0] c; // c represents carry of HA/FA
wire [5:0] s; // s represents sum of HA/FA
// For ease and readability, two diffent name s and c are used instead of single wire name.
genvar g;
generate
for(g = 0; g<4; g++) begin
and a0(p[g][0], A[g], B[0]);
and a1(p[g][1], A[g], B[1]);
and a2(p[g][2], A[g], B[2]);
and a3(p[g][3], A[g], B[3]);
end
endgenerate
assign z[0] = p[0][0];
//row 0
half_adder h0(p[0][1], p[1][0], z[1], c[0]);
half_adder h1(p[1][1], p[2][0], s[0], c[1]);
half_adder h2(p[2][1], p[3][0], s[1], c[2]);
//row1
full_adder f0(p[0][2], c[0], s[0], z[2], c[3]);
full_adder f1(p[1][2], c[1], s[1], s[2], c[4]);
full_adder f2(p[2][2], c[2], p[3][1], s[3], c[5]);
//row2
full_adder f3(p[0][3], c[3], s[2], z[3], c[6]);
full_adder f4(p[1][3], c[4], s[3], s[4], c[7]);
full_adder f5(p[2][3], c[5], p[3][2], s[5], c[8]);
//row3
half_adder h3(c[6], s[4], z[4], c[9]);
full_adder f6(c[9], c[7], s[5], z[5], c[10]);
full_adder f7(c[10], c[8], p[3][3], z[6], z[7]);
endmoduleTestbench Code
// vlsiverify.com
module TB;
reg [3:0] A, B;
wire [7:0] P;
array_multiplier am(A,B,P);
initial begin
$monitor("A = %b: B = %b --> P = %b, P(dec) = %0d", A, B, P, P);
A = 1; B = 0; #3;
A = 7; B = 5; #3;
A = 8; B = 9; #3;
A = 4'hf; B = 4'hf;
end
endmoduleOutput:
Verilog Codes
A = 0001: B = 0000 --> P = 00000000, P(dec) = 0
A = 0111: B = 0101 --> P = 00100011, P(dec) = 35
A = 1000: B = 1001 --> P = 01001000, P(dec) = 72
A = 1111: B = 1111 --> P = 11100001, P(dec) = 225