Wallace Tree Multiplier

Wallace Tree Multiplier (WTA) is a parallel multiplier that works on the Wallace Tree algorithm to efficiently multiply two integers. In this multiplier,

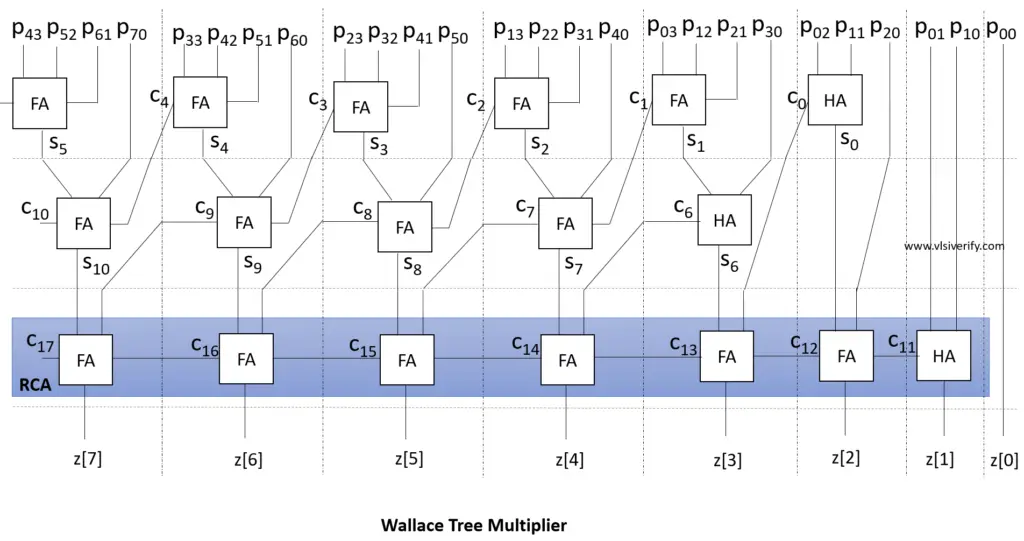
Any three wires with the same weights and input into a full adder. The result will be an output wire of the same weight and an output wire with a higher weight for each three input wires.
If there are two wires of the same weight left, input them into a half adder.
If there is just one wire left, connect it to the next layer.

Advantage: High-speed operation with medium complexity

Disadvantage: Large chip area

Please note of below abbreviations used:

A – holds Multiplicand

B – holds Multiplier

p – Partial Product

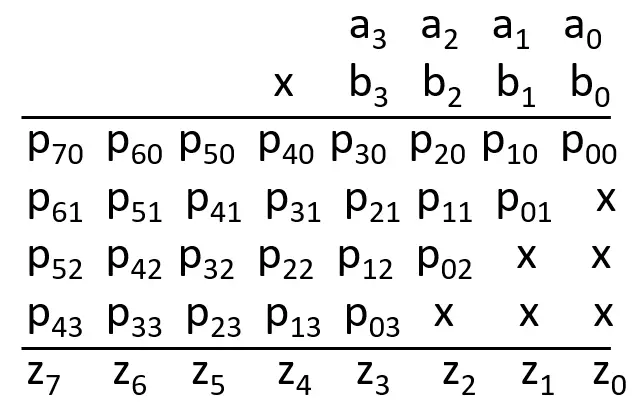
Flow Diagram

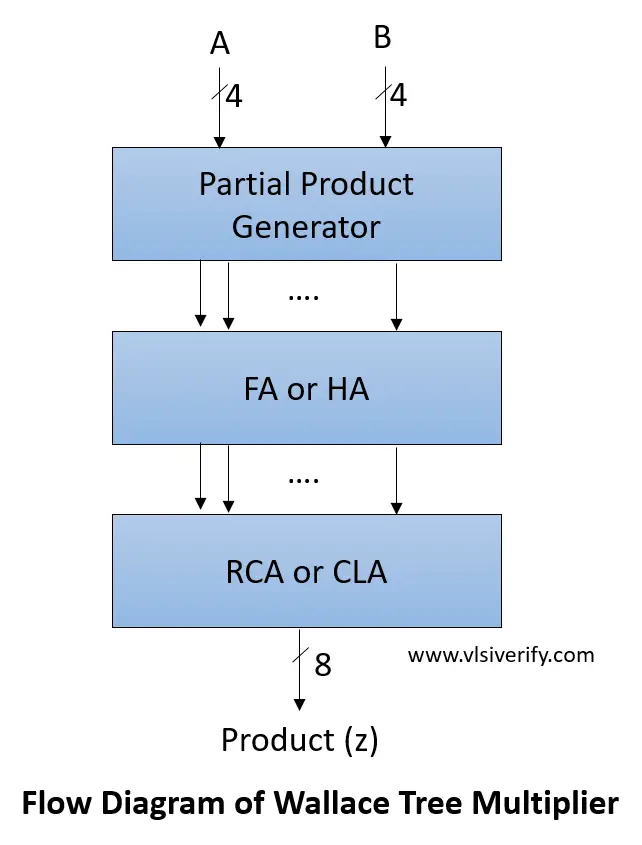
Design Blocks in WTA

The partial product generator generates partial products using a simple two-input AND gate that is fed to the Wallace tree adder.
Multiple half and a full adders that does additions in multiple levels and also considers carry generated by a previous level adder.
The last level of the Wallace tree adder can be implemented ripple carry adder. However, to improve computation latency, a carry look-ahead adder can also be used.

Block Diagram

Wallace Tree Multiplier Verilog Code

module half_adder(input a, b, output s0, c0);
  assign s0 = a ^ b;
  assign c0 = a & b;
endmodule

module full_adder(input a, b, cin, output s0, c0);
  assign s0 = a ^ b ^ cin;
  assign c0 = (a & b) | (b & cin) | (a & cin);
endmodule

// A can hold negative value and B can not hold negative value.
// Below code gives a flavor WTA which can work on negative value as a single argument.
// However, AND, HA and FA can also be reduced if we consider only unsigned values.
module wallace_tree_multiplier(input [3:0] A, B, output [7:0] z);
  reg signed p[8][4];
  wire [17:0] c; // c represents carry of HA/FA
  wire [10:0] s; // s represents sum of HA/FA
  // For ease and readability, two diffent name s and c are used instead of single wire name.
  genvar g;
  reg signed [7:0]M;
  assign {M[7:4],M[3:0]} = {{4{A[3]}},A}; //To extend signed bit till 7th bit
  //always@(M) $display("A=%b, M = %b",A, M);
  
  generate
    for(g = 0; g<4; g++) begin
      and a0(p[g][0], M[g], B[0]);
      and a1(p[g][1], M[g], B[1]);
      and a2(p[g][2], M[g], B[2]);
      and a3(p[g][3], M[g], B[3]);
    end
  endgenerate
  
  //Extra AND gate used for negative number multiplication
  generate
    for(g = 0; g<4; g++) and a4i(p[4][g], M[4], B[g]);
    for(g = 0; g<3; g++) and a5i(p[5][g], M[5], B[g]);
    for(g = 0; g<2; g++) and a6i(p[6][g], M[6], B[g]);
  endgenerate
  and a70(p[7][0], M[7], B[0]);
  
  assign z[0] = p[0][0];

  //row 0
  half_adder h0(p[0][2], p[1][1], s[0], c[0]);
  /*
  //Extended Code
  full_adder f0(p[0][3], p[1][2], p[2][1], s[1], c[1]);
  full_adder f1(p[1][3], p[2][2], p[3][1], s[2], c[2]);
  full_adder f2(p[2][3], p[3][2], p[4][1], s[3], c[3]);
  full_adder f3(p[3][3], p[4][2], p[5][1], s[4], c[4]);
  full_adder f4(p[4][3], p[5][2], p[6][1], s[5], c[5]); // c[5] - not used
  */
  //OR (using generate block)
  generate
    for(g = 0; g<5; g++) full_adder fg0(p[g][3], p[g+1][2], p[g+2][1], s[g+1], c[g+1]);
  endgenerate
  
  //row1
  half_adder h1(s[1], p[3][0], s[6], c[6]);
  /*
  full_adder f5(s[2], p[4][0], c[1], s[7], c[7]);
  full_adder f6(s[3], p[5][0], c[2], s[8], c[8]);
  full_adder f7(s[4], p[6][0], c[3], s[9], c[9]);
  full_adder f8(s[5], p[7][0], c[4], s[10], c[10]); // c[10] - not used
  */
  //OR (using generate block)
  generate
    for(g = 0; g<4; g++) full_adder fg1(s[g+2], p[g+4][0], c[g+1], s[g+7], c[g+7]);
  endgenerate

  //row2
  half_adder h2(p[0][1], p[1][0], z[1], c[11]);
  full_adder f9(s[0], p[2][0], c[11], z[2], c[12]);
  full_adder f10(s[6], c[0], c[12], z[3], c[13]);
  /*
  full_adder f11(s[7], c[6], c[13], z[4], c[14]);
  full_adder f12(s[8], c[7], c[14], z[5], c[15]);
  full_adder f13(s[9], c[8], c[15], z[6], c[16]);
  full_adder f14(s[10], c[9], c[16], z[7], c[17]); // c[17] - not used
  */
  //OR (using generate block)
  generate
    for(g = 0; g<4; g++) full_adder fg2(s[g+7], c[g+6], c[g+13], z[g+4], c[g+14]);
  endgenerate
endmodule

Testbench Code

module TB;
  reg [3:0] A,B;
  wire [7:0] P;
  
  wallace_tree_multiplier wta(A,B,P);
  
  initial begin
    $monitor("A = %b: B = %b --> Product = %b", A, B, P);
    //Note that input A can be signed, but B must be unsigned
    A = 1; B = 0; #3;  // ans = 0
    A = 7; B = 5; #3;  // ans = 35
    A = -5; B = 4; #3; // ans = -20 (Take 2's complement of output)
    A = -3; B = 7; #3; // ans = -21 (Take 2's complement of output)
    A = 9; B = 7; #3;  // (-7)*7 = -49 (Take 2's complement of output)
    A = 7; B = 'hf;    // ans = 105
  end
endmodule

Output:

A = 0001: B = 0000 --> Product = 00000000
A = 0111: B = 0101 --> Product = 00100011
A = 1011: B = 0100 --> Product = 11101100
A = 1101: B = 0111 --> Product = 11101011
A = 1001: B = 0111 --> Product = 11001111
A = 0111: B = 1111 --> Product = 01101001

Verilog Codes